1、直言命题的对当关系
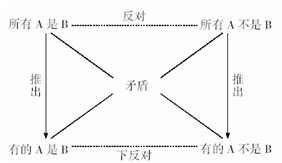
“所有A是B”与“有的A不是B”、“所有A不是B”与“有的A是B”是矛盾关系,必有一真一假。
“所有A是B”与“所有A不是B”是反对关系,必有一假,可以同假。
“有的A是B”与“有的A不是B”是下反对关系,必有一真,可以同真。
一个命题前面加“并非”,等值于这个命题的矛盾命题,即:
并非“所有A是B”=有的A不是B:并非“有的A不是B”=所有A是B
并非“所有A不是B”=有的A是B;并非“有的A是B”=所有A不是B
可简记为:所有与有的互换,有“不”的去掉,没“不”的加上。
2、三段论推理
一特得特:两个前提不能都是特称命题,且只要前提有一个为特称,则结论为特称。特称命题即含有“有的”的直言命题。
一否得否:两个前提不能都是否定命题,且只要前提有一个为否定,则结论为否定。
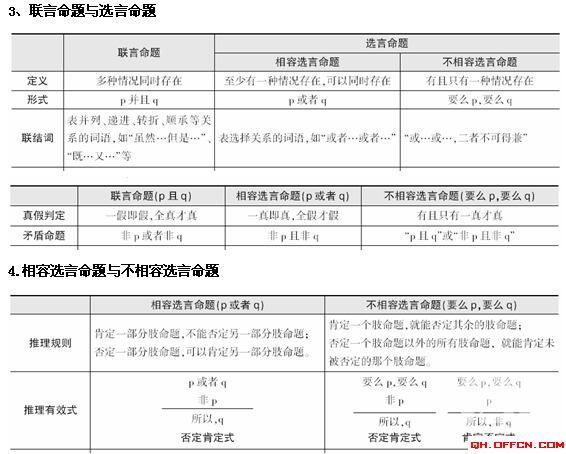
5、假言命题

6、模态命题
并非“必然P”=“可能非P”,即:不必然=可能不;
并非“必然非P”=“可能P”,即:不必然不=可能;
并非“可能P”=“必然非P”,即:不可能=必然不;
并非“可能非P”=“必然P”,即:不可能不=必然。
可简记为:把必然与可能互换,肯定与否定互换。

